İçindekiler
Standart Sapma ve Varyans
Sınıfımızda 30 öğrencinin girdiği ve 30 sorudan oluşan bir sınav yapılmış olsun. Öğrencilerin sınav sonucunda yaptıkları doğru soru sayıları aşağıda görebileceğiniz üzere birbirinden farklı. Sınavda 3 doğru yapan da var 30 doğru yapan da var. Sınıfın (doğru cevap) ortalamasına bakıyoruz 16.87 olmuş. (ortalama = tüm öğrencilerin doğru sayısının toplamı bölü öğrenci sayısı)
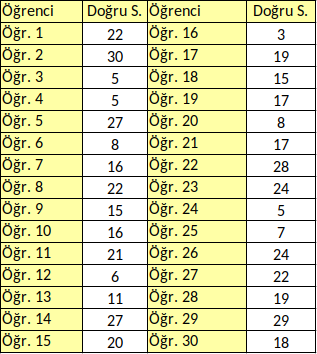
Sizce ortalama 16.87 doğru cevap sayısı, sınıfın genel başarısı açısından bize ne söylüyor? Ortalama olarak / genel olarak sınıfın sınavda sorulan konuları anladığını düşünebilir miyiz?
Örneğimizi ilerletelim; Bir arkadaşınız sınıfa geldi. 100 üzerinden değerlendirilen İktisada Giriş – ECON101 final sınavında sınıfın not ortalamasının 100 üzerinden 50 olduğunu söyledi. Sınıf ortalaması 0 ile 100’üm tam ortasında. Bu sınıfın başarısı, sınavın zorluk derecesi hakkında ne diyebiliriz?
Sınıf Ortalaması neden 50 oldu? Herkes sınavda 50 aldığı için olabilir mi?

Belki de sınıfın yarısı 100 yarısı 0 aldığı ortalama 50 olmuş olabilir mi?
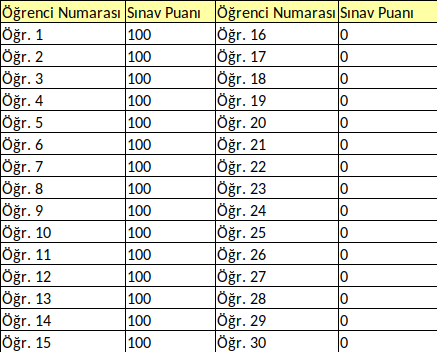
Belki de sınıfın yarısı 75, yarısı 25 aldı. Sonuç olarak ortalama 50 çıktı! Sınıf ortalaması tek başına size bu bilgileri kesin olarak veremez!
Ortalama, bize sınav puanlarının sınıf içinde ne kadar değişkenlik gösterdiğini söylemez. Bunun için ortalamadan başka bir şey bulmak gerekiyor. Öyle bir endeks yaratalım ki ortalamadan ne kadar uzaklaşıldığı, değişkenlik olduğu hakkında bize fikir versin.
Burada biraz daha matematiksel işlem yapacağız;
Önce herkesin sınav puanından, sınıfın ortalamasını çıkaralım. Her öğrenci için ayrı ayrı ortalamadan farkı bulduk. Sonra da bulduğumuz ortalamadan farkları toplayıp, kişi sayısına bölelim. Bir çeşit “ortalamadan farkların” ortalama değerini bulalım.
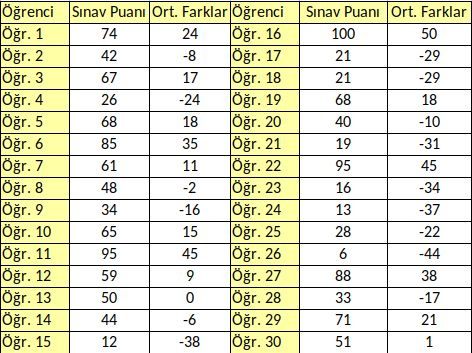
Kimi öğrenci ortalamadan -24 uzaklaşmış kimi öğrenci ortalamadan +45 uzaklaşmış. Bütün bu negatif ve pozitif sayıları topladığımızda ortalamadan farkların toplamı kaç oldu? Kocaman bir sıfır! Sıfırı öğrenci sayısına bölsek yine sıfır. Demek ki ortalamalardan farkların toplamını topladığımızda, toplam her zaman sıfır çıktığı için değişkenlik ölçüsü olarak olduğu gibi kullanamıyoruz.
Burada ufak bir hileye başvuracağız. Negatif ve pozitif sayıların, birbirini götürmemesi için ufak bir hile yapacağız. Teker teker elde ettiğimiz Ortalamadan Farkların Karesini Alarak hepsini pozitif hale getireceğiz.
| Öğrenci | Sınav Puanı | Ort. Farklar | Ort. Farkların Karesi | Öğrenci | Sınav Puanı | Ort. Farklar | Ort. Farkların Karesi |
| Öğr. 1 | 74 | 24 | 576 | Öğr. 16 | 100 | 50 | 2500 |
| Öğr. 2 | 42 | -8 | 64 | Öğr. 17 | 21 | -29 | 841 |
| Öğr. 3 | 67 | 17 | 289 | Öğr. 18 | 21 | -29 | 841 |
| Öğr. 4 | 26 | -24 | 576 | Öğr. 19 | 68 | 18 | 324 |
| Öğr. 5 | 68 | 18 | 324 | Öğr. 20 | 40 | -10 | 100 |
| Öğr. 6 | 85 | 35 | 1225 | Öğr. 21 | 19 | -31 | 961 |
| Öğr. 7 | 61 | 11 | 121 | Öğr. 22 | 95 | 45 | 2025 |
| Öğr. 8 | 48 | -2 | 4 | Öğr. 23 | 16 | -34 | 1156 |
| Öğr. 9 | 34 | -16 | 256 | Öğr. 24 | 13 | -37 | 1369 |
| Öğr. 10 | 65 | 15 | 225 | Öğr. 25 | 28 | -22 | 484 |
| Öğr. 11 | 95 | 45 | 2025 | Öğr. 26 | 6 | -44 | 1936 |
| Öğr. 12 | 59 | 9 | 81 | Öğr. 27 | 88 | 38 | 1444 |
| Öğr. 13 | 50 | 0 | 0 | Öğr. 28 | 33 | -17 | 289 |
| Öğr. 14 | 44 | -6 | 36 | Öğr. 29 | 71 | 21 | 441 |
| Öğr. 15 | 12 | -38 | 1444 | Öğr. 30 | 51 | 1 | 1 |
Teker teker Ortalamadan farkların karesini aldık. Negatif bir şey kalmadı. Hepsi pozitif oldu.
Artık ortalamadan farkların karelerini toplayıp, öğrenci sayısına bölerek “ortalamadan farkların” ortalama değerini ya da “ortalama değişkenliği” hesaplayalım.
| Ortalamadan Farkların Karelerinin Toplamı | 21958 |
| Öğrenci Sayısı | 30 |
| 21958 / 30 | |
| Ortalama Değişkenlik: VARYANS | 731.933333333333 |
Artık ortalamadan sapmaları,farklılıkları açıklayabileceğimiz endeks değerimiz var.
Öğrencilerin genel olarak sınav puanlarının, sınıf ortalamasından 731.9 değişkenlik gösterdiğini bulduk. 731.9 değişkenlik. 731.9?
Nasıl yani 100 puan üzerinden 731 değişkenlik mi? Sınavda 50+731.9 yani 831 puan alan mı var? Tabi ki yok. Yanlış yapmadık.
Hatırlayalım negatif ve pozitif sayıların birbirini götürmemesi için ortalamaladan farkların karesini almıştık. Karelerini aldığımız sayıların sayesinde bulduğumuz ortalama değişkenlik değeri bize varyans yani ortalama değişkenlik değerini vermiş oldu.Sınavın varyans değeri, sınavın maksimum değerinden bile yüksek çıkabilir.
Örneğin ortalamanın 50 olduğu bir sınavda 70 alan bir öğrenci, ortalamadan 20 puan farklı puan almıştır. Biz de o farkın yani 20’nin karesini kullanarak hesaplama yaptık. Kare alma işlemi sonucunda değişkenlik değerini elde ettiğimiz için bulduğumuz değer 731 puan kare olarak okunabilir. Varyans değeri “ortalama değişkenlik değerini” gösteren doğru bir değer olsa da sınav puanı üzerine konuşurken sınav puanın karesi cinsinden yorumlama yapmaya çalışmak kafaları karıştırır. “Sınıfın ortalama değişkenliği 850’dir” derseniz anlaşılması güçtür.
Bunun için bir işlem yapıp karesini aldığımız değerler sonucu elde ettiğimiz varyans değerini eski haline döndüreceğiz. Karekökünü alacağız!
Ta Ta taammm. Ortalamadan değişkenliğin yani varyansın karekökü bize standart sapmayı verdi! 27.05 puan!
- Varyans ve standart sapma arasında ölçüm birimi bakımından fark var.
- Varyans: ölçtüğümüz şeylere ait birim ne ise (boy, kilo,not, yaş v.b.) onun karesi cinsinden bir değerdir. Bizim örneğimizde puan kare diyebiliriz. 731 puan kare ortalamadan değişkenlik.
- Standart sapma: ölçtüğümüz şeyin biriminden hesap yapabileceğimiz bir değer. Bizim örneğimizde 27.05 puan cinsinden ortalamadan değişkenlik. 27.05 puan kadar standarttan sapma da diyebiliriz
Standart sapmanın yüksek veya düşük olmasını nasıl yorumlarız?
Standart sapma kendi başına “iyi” veya “kötü” bir şey değildir. Standart sapma bir değişkenlik göstergesidir. Elimizdeki gözlemlerin, belirli bir aralıkta nasıl dağıldığı hakkında fikir verir. Yeri gelir standart sapmanın yüksek olmasını ya da düşük olmasını isteyebiliriz.
Örneğin bir matematik sınavının sonuçları üzerinden yorum yapalım. Hocanın tüm öğrencilerin dersten geçmesini istediği için çok çok kolay sorular sorduğu, başarısız bir öğrencinin bile yüksek aldığı bir sınavda hem ortalama yüksek çıkar hem de standart sapma düşük çıkar. Şöyle ki sınav çok kolay olduğu için herkes yüksek alır. Herkes yüksek aldığı için sınavın ortalaması yüksek olur. Herkes yüksek ve ortalamaya yakın bir not aldığı için de standart sapma düşük çıkar.
Sadece çalışan öğrencilerin dersi geçtiğinden emin olmak isteyen bir hoca için peki durum nedir? Böyle bir sınavda ortalama 50 olsa da standart sapma yüksek çıkacaktır. Çalışan öğrenciler yüksek puan alır, çalışmayanlar düşük puan alır. Ortalama 50 olur. Fakat standart sapma yüksek çıkar. Standart sapmanın yüksek olması sınav sorularının “başarıyı ölçen” kaliteli sorulardan oluşturduğunu göstermiştir.
Verilerin Dağılımına Bakarak Standart Sapmayı Teşhis Etme
Varyans ve standart sapma bize verilerin dağılımı hakkında da bilgi verir demiştik. Grafikler üzerinden de standart sapma ve varyans hakkında yorum yapabiliriz. Aşağıdaki grafikte sol tarafta bulunan histogram (platykurtic dağılım) standart sapmanın yüksek olduğunu, sağ taraftaki (leptokurtic dağılım) ise düşük olduğunu göstermektedir.
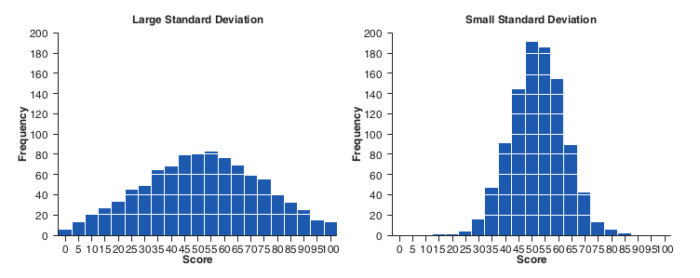
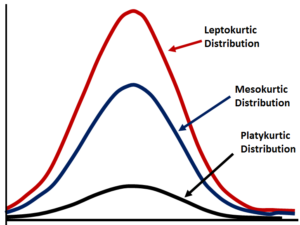
Kendi veri setimize geri dönelim. Sınıf ortalamasının 50 olduğu veri setimizde, standart sapmamız 27.02 çıkmıştı. Standart sapma 10 olsaydı, veriler 50 etrafında leptokurtik şekilde toplanırdı. Dağılım grafiğine baktığımızda gözlemler ortada birikirdi.
Bizim örneğimizde standart sapma 27 gibi bir değer aldı. 100 üzerinden değerlendirdiğimizde oldukça yüksek. Yani platykurtik olma ihtimali fazladır
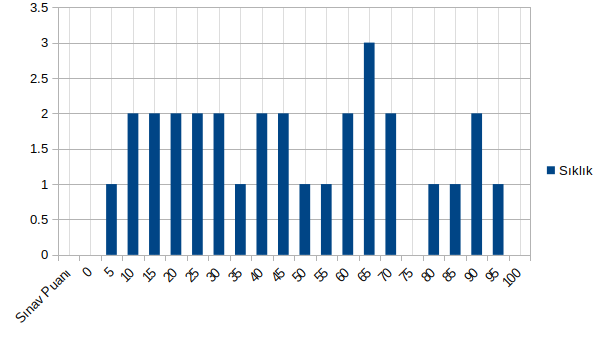
Aşağıdaki histogramda Sınav puanı grafiğimizi beşer puan aralığında sıraladığımızda dağılımın nasıl olduğunu görüyoruz. Kısaca standart sapma yükseldikçe dağılım grafiği şişmanlar. Genişler. Standart sapma azaldıkça ise dikleşmeye leptokurtic olmaya başlar.




Çok güzel ve temiz bi şekilde açıklamışsınız teşekkürler.
bunca sene sonra ilk defa varyansı anladım çok teşekkür ederim
cok teşekkür ediyorum emekleriniz ve bu sade güzel paylaşımınız için.
Rica ederim 🙂
Bir gün öğrencilerim benim anladığım gibi anlasın diye yazmıştım. İşinize yaramasına sevindim 🙂
Katkısı oldu ise ne mutlu 🙂
Çok açıklayıcı, teşekkürler.
Bu kadar açıklayıcı ve kolaylaştıran yazınız için teşekkürler 💯❤️
elllerinize sağlık hocam çok güzel hazırlamışsınız
Sabahtan beri bu içeriğin beğen tuşunu arıyorum. Meğer yorum kısmı burdaymış. Teşekkür ederiz Sefa bey bu net ve sade anlatım için. Varolun.
emek kokan bir yazı olmuş. teşekkür ediyorum.
Mükemmel anlatım teşekkürler
Hocam ,okurken bir yandan daha önce neden bu sayfayı gezmemiş ve okumamışım ki ben dedim . O kadar guzel anladım ki varyans ve standart sapma neymiş, ne işe yarıyormuş. Ellerinize emeğinize sağlık. Ayrıca benim hocalarimdan biri olmanız da ayrı bir gurur verdi ne yalan söyleyim.